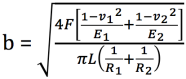Vicsous Shaft Couplings

Most automatic car transmissions use a fluidic coupling to transmit torque. Fluidic couplings have the benefit of controlling the relative speed of two shafts with the shear forces generated in the working fluid (usually Silicone) between a set of discs and the housing. In automatic transmissions, these couplings allow one shaft to spin freely for a brief period of time while gears are changed.

In the case of extreme slip, the fluid heats up and thermally expands. This expansion pushes the discs against each other, nonlinearly increasing their ability to transfer high torques. This self help, called the hump effect, also prevents the coupling from overheating. When the fluid expands under heat, the shafts spin at nearly (if not the exact) same speed, reducing the generation of heat from shear in the fluid.

image and concept taken from Mark’s Standard Handbook for Mechanical Engineers

3D Kinematic Coupling (p-set4)

Repeatable opening and closing of the sample box is important for maintaining a good seal. Kinematic couplings (KCs) are good at ensuring high repeatability, down to the quality of the surface finish in the part. Therefore, this week, I decided to make a mockup of the general shape and size of the box to gain more intuition for the project and practice making a kinematic coupling. For manufacturing simplicity, I decided to go with a 3 V-groove KC. Since the mockup was constructed out of wood, the plate holding the KC balls in place was the largest source of compliance in the structure. The KC box is imaged below.

To test the repeatability of the KC, I taped the box to the floor, taped a laser pointer to the lid, and placed a mark 488″ away from the box. Then my lab-mate removed and replaced the KC lid while I marked the position of the apparent center of the laser. Each time she replaced the lid, she pressed the laser. This introduced an error by deforming the plate on top of the KC balls. In one direction, the angular error was 0.002 radians, and int he other direction, the angular error was 0.005 radians. This happened with the press of a finger, or approximately 0.25 N. This means that the stiffness of the KC is approximately 0.02 radians/N.

However, when the laser was taped on, the force variation from pressing the button was eliminated. The resulting test was far more precise because of the consistent force. In this case, the error was at most (we were limited in accuracy by the width of the laser at that distance) 0.23″ over 488″ or 0.0005 radians.

Protected: Problem = 1/Opportunity (p-set3)

This content is password protected. To view it please enter your password below:

Password:

Adjustable Keys (p-set 3)

If you have every tried to attach something to a shaft before, you know that in the cost-quality-performance triangle of project management, there is not much winning.

• Interference fits require careful design and high tolerance machining, plus they can fail under thermal expansion or centripetal acceleration.
• Pins can induce stress concentrations in the joint, and often require a pin and hole with high tolerances. Plus access to the pin slot can be problematic
• Keys require broaching and also create (albeit smaller) stress concentrations
• Collar clamps can be bulky and hard to integrate into the machine, plus they require compliance
• D-shafts can strip out, and require special machining
• Don’t even get me started in set screws

Each of these joinery methods have advantages too, albeit some have more than others. However, making these joints is often a big part of machine design that can be easily mistaken. So, I decided to go out and see if there are other design elements, lego bricks so-to-speak, that could be added to the list.

Because there are have been many talented engineers working on hard problems throughout history, it did not take me long to find another great way of solving the shaft joinery problem that someone else had thought of: adjusting keys. I found the concept in a book titled Textbook for Vocational Training − Machine Elements and Assemblies and Their Installation by Früngel, Geppert, and Steckling.

A simple adjusting key assembly, from Textbook for Vocational Training.

The assembly works by splitting the shaft collar into two halves, and putting an angle on the back of one of those halves. A key, with a matching angle is inserted into a groove with the angled shaft collar, and held in place with friction, a bolt, or something else depending on the design constraints. At the cost of part count (adding 2-3 components), the design is made less complicated by making the parts out of easily manufacturable geometries. The orientation of the key angle can also be reoriented to suit the application! An excellent tool to keep in the design engineer’s toolbox.

4-Hour Linear Stage (pset-3)

For this week, I decided to practice some rapid-fire-engineering by designing and making an actuated linear stage in 4 hours using 80-20, plastic stock, rope, a stepper motor, a pen and some paper.

 

Protected: Screw Flexures (p-set 2)

This content is password protected. To view it please enter your password below:

Password:

Planar Exact Constraint Toy (p-set 2)

For the planar exact constraint toy, I decided to explore the effect of contact radii and contact stresses on 2D planar pseudo-kinematic couplings (KCs).

Before diving into the toy concept, I briefly want to talk about contact stresses. No two surfaces are perfectly matched. Even if one is molded on the image of the other, there are still imperfections that can arise from oxidation, thermal stresses, body forces, or contaminants. Consequentially, the interface between two surfaces is an amalgamation of point and line contacts. When any force is transmitted across the interface, the point and line contacts (having theoretically zero cross-sectional area) must deform to bear the load at a reasonable stress. In other words, elasticity is the reason why most things fit together or line up (the classic example of this being a 4 legged chair). Taken to another extreme, the contact between two surfaces can be limited to just a few point or line contacts to localize the deformation that must happen to the surfaces to align. If the constrains imposed by the contacts properly matches the desired number of kinematic degrees of freedom, the  interface is considered properly constrained. If there are to few constraints, the interface is under-constrained. If there are too many constraints, it is over-constrained. For an interesting discussions of constraints, flexures and couplings, check out John Hopkins’s  PhD Thesis on FACT and Layton Hale’s PhD Thesis on precision machine design.

I’m calling the structural interfaces in the toy ‘pseudo-kinematic couplings’ because the couplings are over-constrained since that are not perfectly 2D. The third dimension of extrusion turns the point contacts into line contacts. Three perfect line contacts can properly constrain an object, but no line contact is perfect (surface roughness, machining error, etc.) and the interface becomes over-constrained. This is the beauty of creating point contacts between surfaces where at least one surface has positive Gaussian Curvature (or you can be clever and use two cylinders with orthogonally oriented axes, also on the linked wikipedia page). Of course, smaller contact points increase the contact stress and can damage the surfaces. Another example of ‘Conservation of Screwedness’ introduced to me by Professor Oscar Mur-Miranda.

Two quick and important equations on Hertz Contact Stresses for line contacts taken from Professor Alex Slocum’s FUNdaMENTALs, page 17.

Line contact patch size:

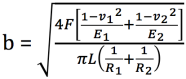
and maximum pressure (stress) along the center of the contact patch:

One very important in the above equation for contact patch size is the 1/R terms in the denominator. They are the radii of curvature for the two contacting surfaces. Small radii make for small contact patches, and large radii (or radii in opposite directions) make for larger contact patches. The contact patch affects the magnitude compression at the interface and the acceptable load that can be transmitted before the damage to the surfaces becomes large.

To explore the role that contact stresses play in KCs, I designed and made a maple plate with identical contact points and different contact radii.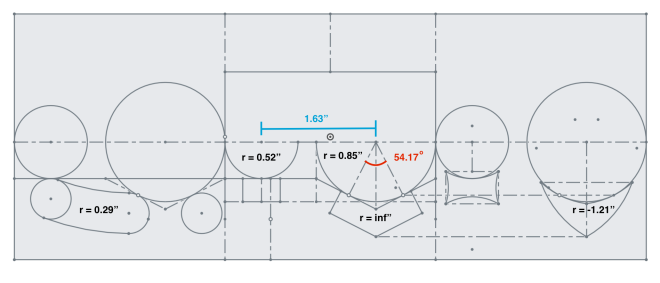 

The analysis for the reaction forces under different loading conditions can be seen here. To explore the effect of contact patch size on any additional friction, this KC was specifically designed to have low lateral load resistance. However, as the vertical load is increased, the reaction forces become able to resist some lateral loading.

Ultimately, the left hand KC (the one with the small circles) felt capable of providing the greatest additional friction against lateral loading. This makes sense, because greater contact stresses dig into the material more. However, without a proper way to control loading (say a spring), there is no way to be rigorous about testing the frictional resistance.

Protected: Sample Box Lit Review/Patent Search

This content is password protected. To view it please enter your password below:

Password:

Protected: Self-Sealing Box FRDPARRC (p-set 2)

This content is password protected. To view it please enter your password below:

Password:

Shear Pin Loading and Failure (p-set 1)

Note: This is this weeks Seek and Geek

I was reviewing my calculations for the strength of a pin in shear, and was finding unsatisfactory reference. Most free-body-diagrams (FBDs) for shear pins do not enforce conservation of momentum. All drawings would begin spinning instead of remaining static. Any FBD that included conservation of momentum did not calculate the bending stresses induced by the internal moment and factor for how that extra stress affects the strength of the pin.

So, I assumed that there is a small amount of slop in the pin causing the pin to contact the joint in small patches. The length of those patches is D/5 (1/5 the diameter of the pin) as a simple St. Venant estimation. Applying a constant distributed load over those patches and applying conservation of linear and rotational momentum on the pin and each handle gives a failure point that is slightly offset from the center of the pin and with an applied force that is 85% the magnitude of a predicted failure force just looking at shear alone. The full calculation is shown in paper below, and will be revised to a cleaner format, such as latex.